Python数据分析--笔记

jupyter notebook常见命令

PS:以下命令都是在命令输入状态下，也即按ESC之后

A:在单元格上方插入新单元格
B:在单元格下方插入新单元格
X:剪切选中的单元格
C:复制选中的单元格
V:粘贴单元格
Z:撤销
M:切换到Markdown输入模式
Y:切换到代码模式
Shift/Ctrl+Enter:执行代码，Shift会在执行完之后在下方新建一个单元格(cell)
Shift+Up/Down:选择上方/下方的cell,可多选
Enter:切换到输入代码模式
ESC:切换到命令模式
%who:查看当前所有变量
%who type:查看type类型的变量，如%who list

example1：随机漫步

from random import choice
import matplotlib.pyplot as plt


class RandomWalk():
    # 定义一个随机行走的类
    def __init__(self, num_points=5000):
        self.x_values = [0]
        self.y_values = [0]
        self.num_points = num_points

    def fill_walk(self):
        # 利用循环来随机填充点
        while len(self.x_values) < self.num_points:
            x_direction = choice([-1, 1])
            x_distance = choice([0, 1, 2, 3, 4, 5])
            x_step = x_direction*x_distance
            y_direction = choice([-1, 1])
            y_distance = choice([0, 1, 2, 3, 4, 5])
            y_step = y_direction*y_distance
            if x_step == 0 and y_step == 0:
                # 若遇到(0,0)零点则重来
                continue
            next_x = self.x_values[-1]+x_step
            next_y = self.y_values[-1]+y_step
            self.x_values.append(next_x)
            self.y_values.append(next_y)


while True:
    # 在不关闭窗口的情况下一直生成随机点
    rw = RandomWalk()
    rw.fill_walk()
    point_numbers = list(range(rw.num_points))
    plt.scatter(rw.x_values, rw.y_values, c=point_numbers,
                cmap=plt.cm.Blues, edgecolor='none', s=15)
    plt.show()
    keep_running = input('Make another walk?(y/n):')
    if keep_running == 'n':
        break

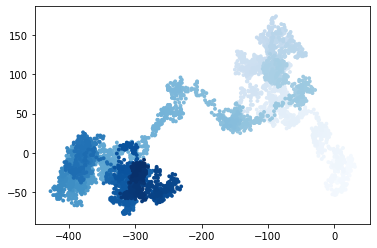
Make another walk?(y/n):y

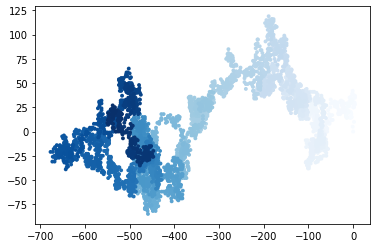
Make another walk?(y/n):n

example2：符号运算

python的符号运算是利用sympy库来实现的。

符号数的定义

$x=Symbol('x')$
$x,y=symbols('x,y')$
$var('x,y')$

第2、3种定义方式都是定义出x,y符号变量

还可以指定符号变量的类型：整型、实型、复数等。

import sympy as sy
x = sy.Symbol('x')
y = sy.Symbol('y')
k, m, n = sy.symbols('k,m,n',integer=True) 
#指定k,m,n为整型
sy.var('z,h')
%who Symbol

h	 k	 m	 n	 x	 y	 z

数学函数的定义

$y=Function('y')$

这实际上是创建了一个类y,该类继承自Function类。而使用y如y(t)相当于创建了y的一个实例,该实例还可以作为整体参与运算

import sympy as sy
f=sy.Function('f')
t=f(x,y)
t**3+2*t

$\displaystyle f^{3}{\left(x,y \right)} + 2 f{\left(x,y \right)}$

求解方程组

求解一元一次方程组

from sympy import *
x = Symbol('x')
e = solve(5*x+x-4, x)
print(e)

[2/3]

求解二元、三元一次方程组

from sympy import *
x, y, z = symbols('x,y,z')
e = solve([x+y-2, x-y+3], [x, y])
print('x={},y={}'.format(e[x], e[y]))
print(solve([x+y+z, x-y-z-3, x+y-z+6], [x, y, z]))
# print('e1={},e2={},e3={}'.format(e1,e2,e3))

x=-1/2,y=5/2
{x: 3/2, y: -9/2, z: 3}

一元二次方程的求解

from sympy import *
x=Symbol('x')
e=solve(x**2-3*x+1,x)
print('x1={},x2={}'.format(e[0],e[1]))

x1=3/2 - sqrt(5)/2,x2=sqrt(5)/2 + 3/2

微积分

求极限

limit运算符：limit(expr,x,a)

表示求 $\lim_{x \to a}expr$

from sympy import *
x = Symbol('x')
e = limit(sin(x)/x, x, 0)
print(e)

求微分

diff运算符： $diff(f,x,n)=f^n(x)$

import sympy as sy
x=sy.Symbol('x')
f=x**2*sy.sin(x)
sy.diff(f,x,2)

$\displaystyle - x^{2} \sin{\left(x \right)} + 4 x \cos{\left(x \right)} + 2 \sin{\left(x \right)}$

解微分方程

$dsolve:dsolve(expr,y(x))$

expr=0,求解y(x)

注意：这个y要事先定义为y=sympy.Function('y')

import sympy as sy
x=sy.Symbol('x',real=True)
y=sy.Function('y')
sy.dsolve(y(x).diff(x)+y(x)**2+y(x),y(x))

$\displaystyle y{\left(x \right)} = - \frac{C_{1}}{C_{1} - e^{x}}$

计算定积分

$integrate:integrate(f,(x,a,b))=\int_a^bf(x)$

import sympy as sy
x=sy.Symbol('x')
sy.integrate(x**2*sy.sin(x),(x,0,1))

$\displaystyle -2 + \cos{\left(1 \right)} + 2 \sin{\left(1 \right)}$

计算不定积分

$integrate:integrate(f,x)=\int f(x)$

import sympy as sy
x=sy.Symbol('x')
sy.integrate(x**2*sy.sin(x),x)

$\displaystyle - x^{2} \cos{\left(x \right)} + 2 x \sin{\left(x \right)} + 2 \cos{\left(x \right)}$

计算双重积分

$integrate(f,(x,x_1,x_2),(y,y_1,y_2))=\int_{x_1}^{x_2}\int_{y_1}^{y_2}f(x,y)dydx$

import sympy as sy
x,y=sy.symbols('x,y')
sy.integrate(3/4*x+2*y*x,(x,0,1),(y,-3,4))

$\displaystyle 6.125$

计算双重不定积分

$integrate(f,x,y)=\int fdxdy$

import sympy as sy
x,y=sy.symbols('x,y')
sy.integrate(x*y,x,y)

$\displaystyle \frac{x^{2} y^{2}}{4}$

算式替换

$subs:expr.subs(x,y)$

将expr表达式中的x替换为y.还可以同时进行多个字母的替换

$expr.subs(\{x:y,t:z\})$

$expr.subs([(x,y),(t,z)])$

但注意以上的操作都不会影响原表达式expr的额值，只是返回一个替换了的表达式

import sympy as sy
x,y=sy.symbols('x,y')
f=x**2+1
print(f.subs(x,y))
print(f)

y**2 + 1
x**2 + 1